Notes
Graphs
Since I work a lot with graphs and talk about them all the time, let’s define what a graph actually is. Here’s a picture of a graph.
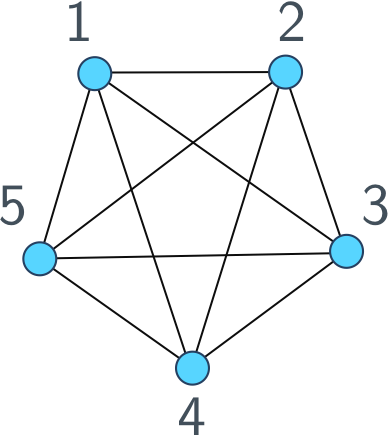
The circles labelled by numbers are called vertices and the links between them are called edges. We only care about the topology of the graph, that is, which vertices are connected and which vertices aren’t. Where they lie in the plane of our drawing doesn’t matter, you can draw a graph however you like as long as the edges respect the connections between vertices.
One way to work with graphs is using an adjacency list: a list of each vertex, followed by its neighbours. For example, we would represent the graph above as
[[1, [2,3,4,5]],
[2, [1,3,4,5]],
[3, [1,2,4,5]],
[4, [1,2,3,5]],
[5, [1,2,3,4]]];